Berechnung der Gravitationskonstante G

Das Gravitationsgesetz besagt, daß sich alle Massen gegenseitig anziehen, daß diese Kraft dem Produkt der Massen proportional ist und indirekt proportional dem Quadrat der Entfernung zwischen den Massen. Die Gravitationskonstante macht aus dieser Beziehung eine Gleichung, sie zählt zu den wichtigen universellen Naturkonstanten. Zur Ermittlung der auch nach Newton benannten Konstante wurden in der Vergangenheit ausschließlich mechanische Verfahren benutzt, die vielen Störgrößen unterliegen, weshalbbisher als Konstante mit großer Ungenauigkeit gilt.

Vergleichsweise ist die Unsicherheit einer Berechnung lediglich durch die Genauigkeit der dabei verwendeten Naturkonstanten bedingt. In der Vergangenheit gab es diverse ergebnislose Versuche zur rechnerischen Bestimmung von[1]. Im folgenden zeigt der Autor auf Basis der in [2], [3] geschaffenen theoret. Grundlagen eine neue Möglichkeit zur rechnerischen Bestimmung der Gravitationskonstante.

Durch Berechnungen rückt eine Reduzierung der Unsicherheit vonum mehrere Zehnerpotenzen in greifbare Nähe. Zunächst erscheint die Ermittlung mittels zwei im Abstandgegenüberstehenden Elektronen naheliegend. Analog zum Coulombschen Gesetz, bei dem sich Ladungen mit unterschiedlichen Vorzeichen anziehen, läßt sich Gravitation als Anziehung entgegengesetzter Pole verstehen, wobei sich Coulombkraftund Gravitationskraftnach Betrag stark unterscheiden:

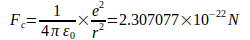
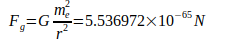
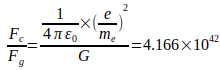
Der Quotient F_c ∕ F_g wird auch als Eddington’s Zahl bezeichnet und selbst für Feynman hatte das Kräfteverhältnis zwischen zwei wechselwirkenden Elektronen große Bedeutung. Der Quotient F_c ∕ F_g kann durch den Term N² ∕ 24 ersetzt werden, wobei N als Large Number bezeichnet wird [2]. Zunächst wird von dem 1986 vom internationalen Codata- Komitee anerkannten 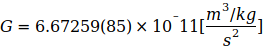ausgegangen [4].

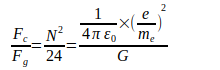
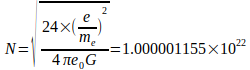(1)

Das Ergebnis läßt erkennen, daß es sich bei der Large Number N um eine große Zahl mit dem Betrag von etwa 1 X 10²² handelt. 1986 waren Angaben wie G = 6.672605 X 10^-11 typisch, wobei die Large Number mit N = 1 X 10²²

ohne nähere Begründung vorausgesetzt wurde [3]. Der Zusammenhang zwischen Masse und Naturkonstanten wird durch die folgende Beziehung definiert, wobei Planckmasse M_o ohne π ∕ 2 Planck ́s Intention von 1900 entspricht. Z₀ ist der Wellenwiderstand des Vakuums [3].

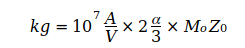
Diese Gl. stellt die Verbindung zu weiteren Naturkonstanten her, ihre Erweiterung bietet die Möglichkeit der Ermittlung von G₀ als Grundlage für Ausgangsdaten zur Bestimmung der Large Number N₀. In der Folge wird für die Feinstrukturkonstante α der Buchstabe b verwendet.

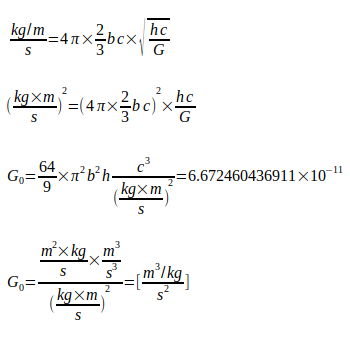 (2)

Der Index 0 bei G₀ bezieht sich auf die Zugrundelegung des Wertes für weitere Berechnungen. Nach Umformung von Gl.(1) erhält man

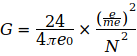
Und durch Substitution von 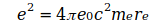entsteht daraus die absolute Minimalvariante einer Gleichung zur Berechnung von G:

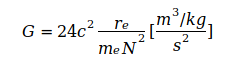 (3)

Durch Gleichsetzung der Gl.(3) mit Gl.(2) kann N gewonnen werden:

Der Index bei N₀ weist auf die Grundlage für weitere Berechnungen hin. Die rel. Unsicherheit von N₀² ist durch die Unsicherheiten der beteiligten Konstanten mit 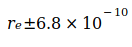, 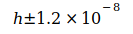und 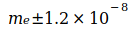bedingt, deren Summe 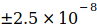beträgt. Von Codata wurden im Zeitraum von 1986 bis 2014 folgende verbindliche Werte zu G veröffentlicht:

Tabelle I

Codata value	Unsicherheit	Datum
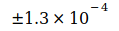		1986
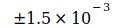		1998
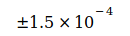		2002
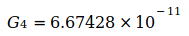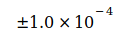		2006
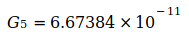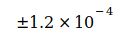		2010
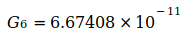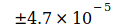		2014

Die Angaben zeigen, daß G im Jahre 2006 ein Maximum erreichte, das in den darauf folgenden Jahren wieder etwas abflachte. Der Gedanke war geboren, diesen abnehmenden Trend auf die Elektronmasse m_e zu beziehen, welche sich nach der umgeformten Gl.(3) aus den Jahresangaben zu G ergibt, also 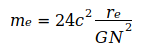. Diese Werte wurden zur präzisen Auswertung auf die in Gl.(2) und Gl.(4) angegebenen Werte G₀ und N₀ bezogen. Damit ergeben sich folgende Abweichungen für die einzelnen Jahreswerte:

Tabelle II

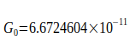	me-bezogene Abweichungen
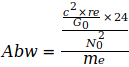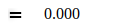		Bezug
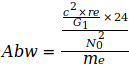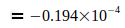		1986
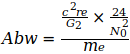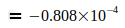		1998
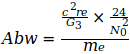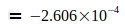		2002
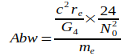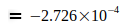		2006
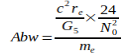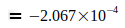		2010
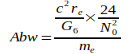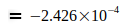		2014

Aus diesen auf die Elektronmasse bezogenen Abweichungen wurde abgeleitet, daß die von Codata angegebene G - Zunahme auch auf eine durch Gl.(3) gegebene m_e - Abnahme zu erklären ist. Es gestaltete sich als schwierig, die einzige dafür infrage kommende Ursache zu finden. Im Zeitraum zwischen 1986 und 2014 reduzierten sich die von Codata für me angegebenen Massen mit 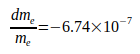auf vernachlässigbare Weise. Es konnte sich also nur um einen Kardinalfehler bei der Ermittlung von G um 1986 handeln, der im Verlauf von Jahren beseitigt wird. Erste Anhaltspunkte ergaben sich aus dem in Fachliteratur viel diskutierten Einfluß der Mitbewegung des Protons beim Wasserstoffatom.

Ein endlich schwerer Kern bewegt sich unter dem Einfluss der Masse des Elektron um den gemeinsamen Schwerpunkt, was für die Rydberg-Konstante R_y Korrektur der Form 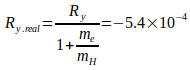zur Folge hat. Gleichzeitig erhöht sich die Masse des Elektron durch seine relativist. Umlaufgeschwindigkeit 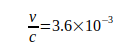, was den Einfluß weiterer, nur unvollständig zu erfassender, Größen aufzeigt [5].

Die Reduzierung der Rydbergkonstante von R_y auf R_yr gilt auch für die Masse des Elektron, da auch gilt: 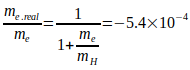. Zur Ermittlung der real wirksamen Rydbergkonstante R_yr wird die von Codata in [6] genannte hydrogen transition frequency zugrunde gelegt: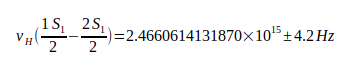(71). Damit ergibt sich die real wirksame Rydbergkonstante R_yr:

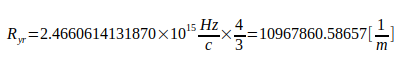
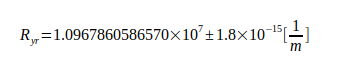
Die Rydbergkonstante R_y gilt als genaueste Naturkonstante überhaupt. Der dimensionslose Quotient Q zwischen ihr und der real wirksamen Rydbergkonstante ist Dreh- und Angelpunkt der Berechnung, er beträgt

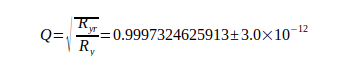(5)
Die Differenz 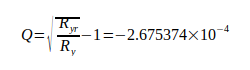entspricht der in der Tabelle II dargestellten m_e - bezogenen Abweichung. Der Vergleich zeigt, daß durch den Quotient die angesprochenen Probleme bei der Nachbildung korrekter Verhältnisse beim H-Atom und ebenfalls bei der Ermittlung von G nach Gl.(3) überwunden werden können. Auf dieser Basis läßt sich die Gravitationskonstante mit den Gleichungen (3), (4), (5) berechnen.

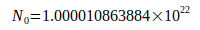
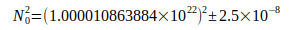
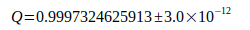
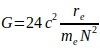
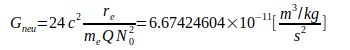(6)

Nunmehr wird untersucht, welche Abweichungen zuverlässige Angaben zu G aus der Literatur gegenüber dem berechneten Wert G_neu haben. Dazu werden in Tabelle III zunächst nur glaubhafte Werte zum Vergleich herangezogen, auch wenn sie teilweise mehrere Jahre zurückliegen:

Tabelle III

Nennwert	Unsicherheit	Herkunft	Jahr	Quelle
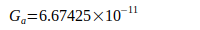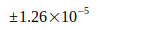		G World	1997	[7]
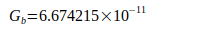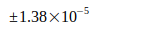		Uni Washington	2000	[7], [4]
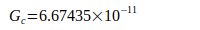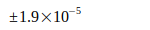		UCI-14 Input	2014	[6]
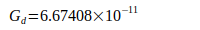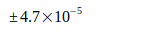		Codata values	2014	[6]

Wie folgende Tabelle IV zeigt, liegen alle Abweichungen dieser Werte gegenüber dem berechneten Wert 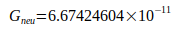innerhalb der von den Autoren angegebenen Unsicherheit. Das Verhältnis von berechneter Abweichung zu Unsicherheit beträgt weniger als eine Standardabweichung.

Tabelle IV

Quotient	Abweichung	Abw./Unsicherheit
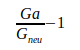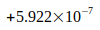		0.047
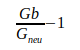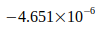		0.337
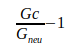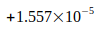		0.797
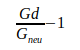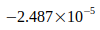		0.529

Ein Ergebnisvergleich der im Jahre 2002 modernsten Angaben nach [7], Tabelle 7.5 mit G_neu zeigt, daß alle darin angegebenen Toleranzen eingehalten werden. Anders ist es bei den von Codata in [6] Table XV gemachten Angaben zu G, wo von 14 Literaturstellen lediglich die folgenden 5 die ihnen zugeordneten Fehlertoleranzen einhalten:

Bagley and Luther (1997) LANL-97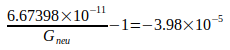
Gundlach and Merkowitz (2000, 2002)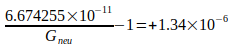
Kleinvoß, Kleinvoß et al. (2002)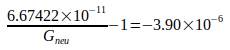
Schlamminger et al. (2006) UZur-06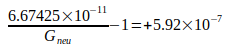
Newman et al. (2014) UCI-14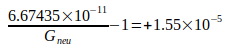

Table XV läßt erkennen, daß von Codata zu G angegebene Werte zum Teil großen Abweichungen unterliegen. Das wird deutlich bei Verwendung des Mittelwertes der 14 enthaltenen Werte mit 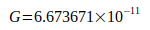anstelle von G_neu, wobei nur 4 von 14 Werten im angegebenen Toleranzbereich liegen.

Zur praxisnahen Berechnung von G ist die Zusammenfassung der unter Gl.(4) und Gl.(5) genannten Ergebnisse zu einer Konstante K sinnvoll.

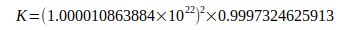
(7)

Aus der abs. Minimalvariante Gl.(3) lassen sich weitere Gleichungen ableiten, indem der Elektronradius r_e einmal durch die Beziehung 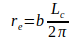und andermal durch die Beziehung 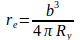ersetzt wird: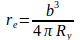

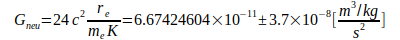
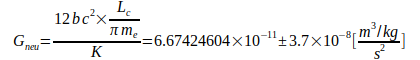
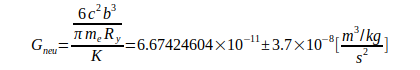
Die Unsicherheit bei der Berechnung von G wird vorwiegend durch N₀² nach Gl.(4) bzw. die Konstante 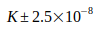nach Gl.(7) bestimmt. Dazu kommt bei Gl.(3) noch die Unsicherheit der Elektronmasse 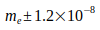.Die Ungenauigkeit der noch beteiligten Konstanten kann vernachlässigt werden. ( 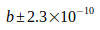, , 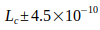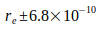). Die Unsicherheit der Elektronmasse m_e bestimmt also den Gesamtfehler der G - Berechnung.

Eigentliche Ursache der Ungenauigkeit von m_e ist die zugrundeliegende Avogadro- Konstante mit 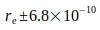, wodurch eine weitere Erhöhung der Genauigkeit von G begrenzt wird. Prinzipiell ist die Genauigkeit von G auf das 3-fache der für N_A geltenden Unsicherheit begrenzt. Durch SI-Bestrebungen ist Angleichung auf 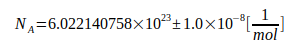geplant [8], was künftige Genauigkeits- Grenzen von G deutlich macht.

DAS G- FELD IST ENERGIE ! FOLGLICH EXISTIERT KEIN „LEERER“ RAUM. AUCH DAS ELEKTRON LIEFERT SEINEN BEITRAG..... (M. Geilhaupt)

Den Berechnungen liegen folgende Naturkonstanten zugrunde:

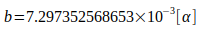
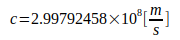
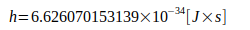
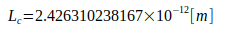
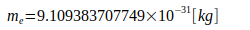
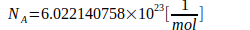
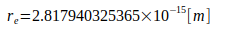
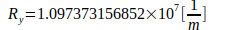
Literature

1.  E. Suckert: Über Natur des Elektrons und Ursache der Gravitation, 2013
2.  Prof. Dr. Manfred Geilhaupt: Fundamental Unit Momentum, 1986
3.  Prof. Dr. Manfred Geilhaupt: Basic Units of Physics, 1984
4.  Prof. Dr. Wolschin: Schwierige Bestimmung einer Naturkonstante, 2001
5.  Samuel Miesch: Atomare Spektren - Bohrsches Atom- Modell, 2003
6.  CODATA: Recommended Values of the Fundamental Physical Constants, 2014
7.  Ulf Kleinevoß: Bestimmung der Newtonschen Gravitationskonstante,2002
8.  David Newell: The CODATA 2017 values for the revision of the SI, 2018

Dipl.-Ing. (FH) Kurt Vogel
Email: kurt.vogel@gmx.de
Datum: 30.04.2019

 

Gravitationskonstante